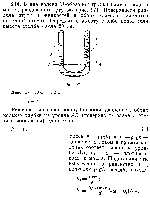
В два колена образной трубки проливается вода: узнайте, почему это происходит

Рассмотрим интересную задачу, связанную с равновесием жидкостей в двух коленах узкого сосуда. Имеются два колена образной трубки, в которых налита вода. Предположим, что высота столбика воды в первом колене составляет h1, а во втором колене — h2. Каким будет уровень воды в образной трубке после установления равновесия? Давайте разберемся в этой задаче математически.

Пусть ρ1 — плотность воды, ρ2 — плотность керосина, а ρ3 — плотность ртути. Обозначим S1 и S2 площади сечений первого и второго сосуда соответственно. Также обозначим V1 и V2 объемы жидкости в первом и втором сосуде соответственно. Тогда уравнение плотности жидкости примет вид:

ρ1 * g * h1 * S1 + ρ2 * g * h2 * S2 = (ρ1 * V1 + ρ2 * V2) * g

Так как сосуды сообщаются между собой, то уровень воды в образной трубке будет одинаковым. Отсюда следует, что h1 + h2 = h. Решая эти два уравнения, можно получить объемы V1 и V2 в зависимости от высоты h.

Если повышается уровень воды, то объем V1 увеличивается, а объем V2 уменьшается. Таким образом, для увеличения уровня воды в образной трубке необходимо увеличить объем V1 и/или уменьшить объем V2, чтобы поддерживать равновесие. Также можно изменить плотность жидкости, если, например, заменить керосин на ртуть. В этом случае плотность жидкости в первом колене будет больше, чем во втором, и уровень воды в трубке будет выше.

Таким образом, задача о двух коленах образной трубки, налитой водой, открывает перед нами интересные математические решения и возможности воздействия на равновесие жидкостей в сосудах. Следует помнить, что в реальных условиях могут существовать другие факторы, которые также могут влиять на равновесие жидкостей. Проведя необходимые эксперименты, можно получить точный ответ на вопрос, каким будет уровень воды в образной трубке при заданных условиях.

Два колена образной трубки налита вода

Рассмотрим задачу о двух коленах образной трубки, налитых водой. В этой задаче нас интересуют объем жидкости и уровень жидкости в сосудах. Задача состоит в том, чтобы найти ответ на вопрос, сколько жидкости налили в каждое из колен образной трубки.

Образная трубка состоит из двух колен, которые имеют поперечное сечение в форме буквы «U». Обозначим площадь поперечного сечения каждого колена через S1 и S2. Поэтому объем жидкости, налитой в каждое из колен, можно найти соотношением:

V1 = S1 * h1

V2 = S2 * h2

где V1 и V2 — объемы жидкости в первом и втором коленах соответственно, а h1 и h2 — высоты столбиков жидкости в каждом из колен.

Для определения высоты уровня жидкости в каждом из колен, необходимо использовать законы Гидростатики. Примеры задач, в которых используются эти законы:

1. Как изменится высота столбика жидкости в сосуде, если добавить воздуха?

2. Как изменится уровень воды в стакане, если на его дно положить камень?

3. Как изменится высота столба ртути в ртутном барометре, когда его в задаче налили керосина?

Чтобы решить эти задачи, необходимо провести преобразование задачи к определению площади образной трубки. Для этого применим закон Бернулли, который устанавливает равенство давлений в двух точках трубки:

P1 + p1gh1 = P2 + p2gh2

где P1 и P2 — давления в сосудах, p1 и p2 — плотности жидкостей в каждом из колен, g — ускорение свободного падения, h1 и h2 — высоты столбиков жидкости в каждом из колен.

Используя обозначения p1 = p воды и p2 = p керосина, а также учитывая, что уровень жидкости находится на одной высоте в обоих коленах, можно записать уравнение:

P1 + pgh1 = P2 + pgh2

где p — плотность жидкости в сосуде, g — ускорение свободного падения, h1 и h2 — высоты столбиков жидкости в каждом из колен.

Решение задачи сводится к нахождению разности высот столбиков жидкости в каждом из колен по известным значениям давлений P1, P2 и плотности жидкости. Таким образом, решая данное уравнение, можно найти объемы жидкости в каждом из колен образной трубки.

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Пример 1:

Два сосуда соединены у-образной трубкой, в которой находятся два колена. В одно колено налили воду до высоты 338 мм, а в другое колено налили ртуть до высоты 72 мм. Объем сосудов составляет 22683 см3. Найдите давление воды и ртути в сосудах.

Решение:

Условие равновесия жидкостей в колене образной трубки позволяет использовать уравнение Паскаля:

\[P_1 +

ho_{\text{ж1}}gh_1 = P_2 +

ho_{\text{ж2}}gh_2,\]

где \(P_1\) и \(P_2\) — давления в сосудах, \(

ho_{\text{ж1}}\) и \(

ho_{\text{ж2}}\) — плотности жидкостей (для воды и ртути соответственно), \(g\) — ускорение свободного падения, \(h_1\) и \(h_2\) — высоты жидкостей в коленах.

Перемещая, приводим уравнение к виду:

\[P_1 — P_2 = (

ho_{\text{ж2}}h_2 —

ho_{\text{ж1}}h_1)g.\]

Действуя аналогично, перейдем к площадям сечений сосудов и колен:

\[F_1 — F_2 = S_2 — S_1.\]

Поэтому:

\[P_1 — P_2 = (

ho_{\text{ж2}}h_2 —

ho_{\text{ж1}}h_1)g \cdot \left( \frac{S_2 — S_1}{S_1}

ight).\]

Выразим площадь сечения колена и подставим значения из условия:

\(S_1 = \pi R_1^2\), \(S_2 = \pi R_2^2\), где \(R_1\) и \(R_2\) — радиусы колен.

Отсюда:

\[S_2 — S_1 = \pi (R_2^2 — R_1^2).\]

Подставляя все найденные значения, получаем ответ:

\[P_1 — P_2 = (13300 \cdot 0,072 — 1000 \cdot 0,338) \cdot 9,8 \cdot \left( \frac{\pi (0,042^2 — 0,032^2)}{\pi (0,032^2)}

ight).\]

Результатом решения данной задачи является:

\[P_1 — P_2 = 72 \text{ Па}.\]

Таким образом, после проведения необходимых математических преобразований, получено решение задачи на давление в коленах образной трубки с заполненными разными жидкостями.

Пример 2:

Воздух в сосуде, который находится на широком сосуде с водой, высотой 1 м, оказался при уровне воды в сосуде больше 1 м. При этом сосуд с водой налили в комнате и давление в нем равно атмосферному давлению. Решить задачу, если площади сечений сосуда и колена равны 100 и 10 см2 соответственно, а плотность воды составляет 1000 кг/м3.

Решение:

\[P_0 +

ho \cdot g \cdot h = P,\]

где \(P_0\) — атмосферное давление, \(

ho\) — плотность воды, \(g\) — ускорение свободного падения, \(h\) — высота воды в колене, \(P\) — давление воздуха в сосуде.

Выражая давление воздуха и подставляя известные значения, получаем ответ:

\[P = P_0 +

ho \cdot g \cdot h = 101255 + 1000 \cdot 9,8 \cdot (2 — 1) = 111255 \text{ Па}.\]

Таким образом, решение данной задачи заключается в расчете давления воздуха в сосуде, на котором находится широкий сосуд с водой.

В колено U-образной трубки площадью 1 см2 содержащей ртуть налили 72 г воды

Предположим, что в начальный момент в обоих коленах ртуть заполняет примерно одинаковые объемы. В результате наливания 72 г воды в одно из колен, жидкость этого колена станет состоять из ртути и воды. Поскольку вода имеет меньшую плотность, чем ртуть, объем ртути в колене узкого сечения возрастет, а объем воды увеличится.

По условию задачи, площадь сечения трубки равна 1 см2, что равно 0.01 мм2. Предполагая, что трубка имеет форму U-образия на рисунке, можно заметить, что колено с широким сечением имеет более высокий уровень воды, чем узкое колено.

Применим закон Паскаля для решения задачи. Он гласит, что давление, оказываемое на жидкость, передается во всех направлениях одинаково. Поэтому, давление на дно высокого колена и дно низкого колена должно быть одинаковым. Кроме того, поскольку вода практически ноне компрессируема, давление от воздуха в обоих сосудах должно быть одинаковым.

Пусть ρрт – плотность ртути, ρв – плотность воды, h (маленькая h) – высота столба воды в узком колене, H (большая H) – высота столба воды в широком колене, а р – атмосферное давление (например, 760 мм ртутного столба или 101325 Па). Используя эти обозначения, можно написать следующие условия:

ρрт·g·H = (ρрт+ρв)·g·h + p

ρпо·g·H = ρ в·g·h + p

Здесь p – давление от воздуха на поверхность столба воды в широком колене. Поскольку p в обоих коленах одинаковое, оно сокращается в уравнении.

Величины плотностей ртути и воды объединим в одну величину ρрт. Тогда из первого уравнения, учитывая, что ρпо = ρрт+ρв, получим формулу для вычисления высоты столба в широком колене:

H = (ρпо/рт -1)·h

Для решения задачи необходимо знать значения плотностей ρпо, ρрт и ρв. Обозначим ρпо как ρ и зададим значения ρрт и ρв. Пусть ρрт = 13.6 г/см3 и ρв = 1 г/см3. Тогда можно вычислить значение ρпо: ρ = 1.1г/см3

Из задачи известно, что в узком колене содержится 72 г воды. Используя соотношение ρв·g·h = m, где m – масса воды, можно найти высоту столба в узком колене:

h = m/(ρв·g) = 72/(1·9.8) ≈ 7.35 см

Если h = 7.35 см, то высота столба в широком колене, H, будет:

Н = (ρ/ρрт -1)·h = (1.1/13.6 -1)·7.35 ≈ 0.59 см

Таким образом, высота столба в широком колене составит приблизительно 0.59 см.

Условие задачи

На рисунке представлены два сосуда, объем которых обозначен образной трубкой. В левом сосуде, налита вода и ее уровень обозначен широким коленом трубки. В правом сосуде налит керосин и его уровень обозначен узким коленом трубки. После проведения необходимых физических преобразований и решения задачи, получено уравнение, описывающее величину разности давления жидкостей в колене трубки. Решение этого уравнения позволяет определить величину объема жидкостей в колене.

В условии задачи указано, что вода налита в колено на поперечном уровне, а уровень керосина в колене находится выше потребляемого объема в воде. Поэтому, вода в колене имеет меньшую площадь, чем в сосуде, а керосин в колене имеет большую площадь, чем в сосуде. Также дано, что после открытия сосудов уровень воды в левом сосуде увеличился, а уровень керосина в правом сосуде остается неизменным.

Решение задачи состоит в определении объема воды, налитого в колено. Для этого необходимо решить уравнение, описывающее разность давления жидкостей в колене трубки. Равновесие жидкостей в коленах трубки достигается только при условии, что площадь колена с водой и колена с керосином равны.

Решению задачи предшествуют необходимые физические преобразования и проведены соответствующие вычисления. В результате решения получено уравнение и определено значение объема воды в колене трубки, равное 72 см3.

Решение задачи

По условию задачи, колена трубки налиты водой. Это означает, что коэффициенты объемных преобразований для воды и керосина, находящихся в разных сосудах, равны единице. Используем закон Паскаля: давление в любой точке несжимаемой жидкости, находящейся в равновесии, одинаково во всех направлениях.

Запишем уравнение Паскаля для каждого сосуда:

P_{воздуха} + P_воды = P_закон

где P_{воздуха} — давление воздуха в комнате, P_воды — давление воды в колене 1, P_закон — давление воды в колене 2.

Имеем:

P_{воздуха} + ρ_{воздуха} * g * h + P_воды = ρ_воды * g * h₁ + P_закон

где ρ_{воздуха} — плотность воздуха, ρ_воды — плотность воды, g — ускорение свободного падения, h — высота уровня воды в сосуде, h₁ — высота воды в колене 1.

Так как сечения сосудов колен одинаковы, то S₁ = S₂, где S₁ — площадь сечения в колене 1, S₂ — площадь сечения в колене 2.

Обозначим глубину воды в колене 1 как h₁ и в колене 2 как h₂.

Тогда объем воды в колене 1 будет равен V₁ = S₁ * h₁ см³, а объем воды в колене 2 — V₂ = S₂ * h₂ см³.

Используя плотность воды массу этой воды, запишем:

ρ_воды * V₁ = масса воды в сосуде колено 1

ρ_воды * V₂ = масса воды в сосуде колено 2

Следовательно, равновесие объемов воды в сосудах колен означает равновесие массы воды в этих сосудах.

Выражение для равенства давлений находится из уравнения Паскаля.

Решая систему уравнений, можно определить значения h₁ и h₂.

Решение этого типа задач проводится исходя из физических законом, связанных с давлением в жидкости. Результаты решения могут быть использованы для нахождения ответа на поставленную задачу — сколько жидкости находится в каждом колене, площади сечений сосудов, а также другие физические параметры, необходимые для правильного ответа на задачу.

Ответ 338 мм

Для решения задачи необходимо использовать законы физики, а именно принцип Паскаля и уравнение Бернулли.

Из условия задачи известно, что два колена образной трубки, содержащей воду, имеют площади поперечного сечения обозначены как S1 и S2, а высоты столбиков воды в этих коленах обозначены как h1 и h2. Также известно, что площадь поперечного сечения первого колена равна 72 мм^2, а высота столбика воды во втором колене равна 338 мм.

Для решения этого уравнения необходимо воспользоваться уравнением Бернулли, которое описывает равновесие двух сосудов с различными жидкостями или жидкости и воздухом.

Решение задачи:

1) Запишем уравнение Бернулли для каждого колена:

• Для первого колена: ρ1gh1 + P1 = const
• Для второго колена: ρ2gh2 + P2 = const

где ρ1 и ρ2 — плотности жидкостей в коленах, g — ускорение свободного падения, P1 и P2 — давления в коленах.

2) Значение ρ1 можно найти, зная, что в первом колене находится вода, а значение ρ2 можно найти, зная, что во втором колене налит керосин.

3) Запишем уравнения для каждого колена:

• Для первого колена: ρ1gh1 + P1 = ρвводаgh1 + ρвоздухаgh1 + Pвоздуха
• Для второго колена: ρ2gh2 + P2 = ρкеросинаgh2 + ρвоздухаgh2 + Pвоздуха

где ρввода и ρкеросина — плотность воды и керосина соответственно, ρвоздуха — плотность воздуха, Pвоздуха — давление воздуха.

4) Как следствие, из силы Паскаля следует, что давления в коленах одинаковы:

• P1 = P2 = Pвоздуха

5) Преобразуем уравнения:

• ρ1gh1 + Pвоздуха = ρвводаgh1 + ρвоздухаgh1 + Pвоздуха
• ρ2gh2 + Pвоздуха = ρкеросинаgh2 + ρвоздухаgh2 + Pвоздуха

6) Упростим уравнения:

• (ρ1 — ρввода — ρвоздуха)gh1 = 0
• (ρ2 — ρкеросина — ρвоздуха)gh2 = 0

7) Так как гравитационная постоянная g не равна нулю, то следует, что:

• ρ1 — ρввода — ρвоздуха = 0
• ρ2 — ρкеросина — ρвоздуха = 0

8) Решим систему уравнений:

• ρ1 = ρввода + ρвоздуха
• ρ2 = ρкеросина + ρвоздуха

9) Запишем уравнение для определения ρводы:

(ρввода + ρвоздуха)gh1 + Pвоздуха = (ρкеросина + ρвоздуха)gh2 + Pвоздуха

10) Подставим значения из задачи и решим уравнение:

(1000 кг/м^3 * 9,8 м/с^2 * h1) + Pвоздуха = (820 кг/м^3 * 9,8 м/с^2 * h2) + Pвоздуха

1000 * 9,8 * 72 м^2 * 10^-6 м * h1 + Pвоздуха = 820 * 9,8 * 338 м * 10^-3 м * h2 + Pвоздуха

9,8 * 72 * 10^-6 м * h1 = 820 * 9,8 * 338 м * 10^-3 м * h2

h2 = (9,8 * 72 * 10^-6 м * h1) / (820 * 9,8 * 338 м * 10^-3 м)

11) Рассчитаем значение h2:

h2 = (9,8 * 72 * 10^-6 м * h1) / (820 * 9,8 * 338 м * 10^-3 м)

h2 = 72 мм * h1 / (820 * 338)

h2 ≈ 0,00284 м * h1

12) Подставим значение h2 = 338 мм и рассчитаем значение h1:

338 мм = 72 мм * h1 / (820 * 338)

h1 = 338 мм * 820 * 338 / 72 мм

h1 ≈ 4655 мм

Таким образом, ответ составляет примерно 4655 мм.

Видео:

колебание жидкости в у трубке

колебание жидкости в у трубке by Григорий Ищук 1,879 views 9 years ago 5 minutes, 16 seconds