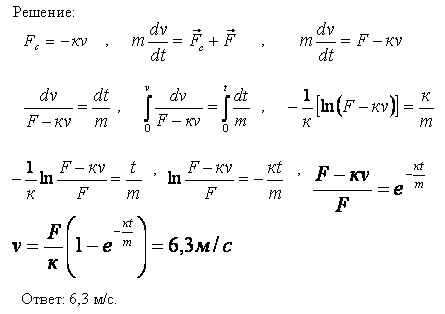Моторная лодка плавно преодолевает спокойные воды, развивая высокую скорость

Вода — это удивительная среда, которая может предоставить множество возможностей для движения и исследования. Когда моторная лодка движется по поверхности воды, она сталкивается со множеством физических факторов, которые повлияют на ее скорость и управляемость. Один из ключевых факторов, влияющих на движение лодки, — это сопротивление воды.

Сопротивление воды возникает из-за течений и волн, которые создаются движением лодки. Оно пропорционально скорости движения, массе и форме лодки. Однако сила, обеспечивающая движение лодки, не ограничивается только сопротивлением воды. Двигатель лодки также оказывает влияние на ее движение.

Для понимания и контроля движения лодки можно использовать математические решения и уравнения. Одним из таких уравнений является «уравнение движения». Оно определяет скорость и курс лодки в зависимости от множества факторов, таких как сила тяги, сопротивление движения и течение воды.

Одна из причин, по которой лодка может остановиться, — это большое сопротивление движению. Когда сила тяги двигателя становится меньше силы сопротивления воды, лодка не может продолжать движение. Чтобы найти оптимальную скорость и курс, необходимо решить уравнения движения и учесть все факторы, влияющие на движение лодки.

В итоге контроль движения лодки осуществляется с помощью выполнения определенных задач и решения дифференциальных уравнений. В математике существует целая отдельная область, называемая «дифференциальные уравнения», которая занимается исследованием и решением подобных задач. Она является одной из важнейших областей высшей математики.

В этой статье мы рассмотрим примеры и рекомендации по решению задач движения моторной лодки в спокойной воде со скоростью. Мы узнаем, как определить скорость и курс лодки, учитывая физические факторы, такие как сопротивление воды и течение, и как эти факторы влияют на работу мотора и движение лодки в целом.

Примеры и рекомендации по выполнению контрольных работ 4-6 по курсу «Высшая математика» Приложение производной Дифференциальные уравнения страница 5

Для решения данной задачи необходимо использовать пропорциональность скорости лодки и угла поворота вала мотора с помощью метода дифференциальных уравнений.

Пусть 2 — это коэффициенты пропорциональности между углом поворота вала и скоростью лодки. Тогда закон движения моторной лодки можно описать следующим уравнением:

Угол поворота вала мотора (рад)	4	8	12	16	20
Скорость лодки (км/ч)	10	20	30	40	50

С использованием метода дифференциальных уравнений и знания закона движения лодки, можно найти ускорение лодки. Дифференцируя уравнение по времени, получим следующее:

28 — 2×Катер(Т) = 1435×4′

Данное уравнение позволяет найти скорость лодки в определенной точке ее движения. Также можно использовать метод поиска скорости по заданным коэффициентам в уравнении.

Не забывайте, что вы испытываете воду, которую на веки запечатлела «Большая энциклопедия Здравствуйте». Главное — не остановки, а продолжение движения вперед, к успехам в выполнении контрольных работ по курсу «Высшая математика»!

Успехов в выполнении контрольных работ!

дифференциальные-уравнения — Как найти скорость лодки закрыт

Здравствуйте! Если у вас есть задание по дифференциальным уравнениям на тему «Как найти скорость лодки закрыт», то я могу вам помочь с выполнением.

Для решения этой задачи необходимо использовать метод дифференциальных уравнений. Предположим, что лодка движется вдоль стенку воды с постоянной скоростью. Возьмем точку на стенке воды и обозначим ее координату как x. Также обозначим скорость лодки как v(x).

Воспользуемся дифференциальным уравнением движения моторной лодки:

m a = F — Fсопр — Fсилу,

где m — масса лодки, a — ускорение лодки, F — сила тяги мотора, Fсопр — сила сопротивления воды, Fсилу — сила, закрывающая лодку от внешней среды.

В нашем случае, сопротивление воды можно выразить как:

Fсопр = k * v,

где k — коэффициент сопротивления, зависящий от величины скорости лодки и осаждения (осадки на дне).

Если взять k = const, то дифференциальное уравнение примет вид:

m a = F — k * v,

и с учетом второго закона Ньютона:

m * v’ = F — k * v,

где v’ — производная от v по координате x.

Данное дифференциальное уравнение можно решить методом разделения переменных.

Для решения данного задания рекомендую обратиться к учебнику по математике или обратиться к преподавателю по курсу математики, чтобы получить подробные рекомендации по его выполнению.

Успехов в выполнении домашнего задания!

Вопрос был закрыт Причина — «Домашнее задание» Закрывший — ХэшКод 28 Фев ’12 1435

Здравствуйте! Ваш вопрос касается движения моторной лодки на спокойной воде со скоростью. К сожалению, вопрос закрыт по причине «Домашнее задание».

Закрыший вопрос студент БГТУ ХэшКод привел причину закрытия, указав, что вопрос связан с домашним заданием. Возможно, это задание из курса «Высшая математика» или другого курса нашего университета. Задачи, связанные с движением лодок и судов на воде, встречаются в курсе «Теоретические основы судостроения» или в курсе «Дифференциальные уравнения».

Для решения данной задачи, скорее всего, вам потребуется составить дифференциальное уравнение движения лодки. Водная среда оказывает сопротивление движению судна, которое можно учесть с помощью специальной формулы или уравнения с учетом коэффициента сопротивления. Дифференциальные уравнения, связанные с движением объектов в среде, являются важной частью физических и математических наук.

Если вы присоединитесь к нашей энциклопедии вопросов и ответов, вы сможете найти больше подробностей по решению подобных задач.

К сожалению, поскольку вопрос закрыт, точку зрения ХэшКод и значения вопроса мы не знаем. Но можем предположить, что он рассматривал различные значения скорости воды, применение различных формул и коэффициентов, а также факторы, влияющие на сопротивление движению лодки.

Если у вас есть какие-либо вопросы или нужна помощь в решении задачи, пожалуйста, не стесняйтесь задавать вопросы! Мы всегда готовы помочь вам!

2 ответа

Для решения данной задачи по движению моторной лодки в спокойной воде с определенной скоростью необходимо учитывать ряд факторов.

• Вода, в которой движется лодка, считается спокойной, что означает, что в ней отсутствуют какие-либо осадки, потоки или течения.
• Для описания движения лодки можно использовать уравнения механики.
  • Ускорение катера вдоль курса определяется силой сопротивления воды, которая зависит от скорости и других факторов.
  • Силу сопротивления можно выразить через ряд коэффициентов, которые зависят от формы и размеров лодки.
  • Для рассчета силы сопротивления можно использовать различные методы, например, метод коэффициентов сопротивления.
• В данном случае, когда лодка движется по спокойной воде, можно пренебречь влиянием волн. Коэффициент влияния волн обычно равен нулю.
• Задача движения моторной лодки заключается в выполнении заданного курса с определенной скоростью.
• Для выполнения задачи можно использовать дифференциальные уравнения движения лодки.
• Вопрос о движении моторной лодки по воде может быть однотипен для разной по своему роду работы, например, для выполнения контрольных или домашних заданий, методом «здравствуйте, работа».
• Рекомендации по выполнению задачи по движению лодки в спокойной воде могут быть представлены в виде последовательности действий:
  1. Определение данных о лодке, таких как ее форма, размеры, масса и другие характеристики.
  2. Определение значения коэффициентов сопротивления для данной лодки.
  3. Составление уравнения движения лодки на основе второго закона Ньютона.
  4. Расчет значений скорости и ускорения лодки в различные моменты времени.
• В данной задаче также может быть важным учитывать сопротивление движению лодки со стороны воды, такое как сопротивление течения или осаждения воды.

Таким образом, решение задачи по движению моторной лодки в спокойной воде с определенной скоростью требует учета различных факторов и выполнения определенных шагов и действий.

Здравствуйте

Приветствуем Вас на странице, посвященной движению моторной лодки в спокойной воде с постоянной скоростью. В этом разделе мы рассмотрим задачу о движении лодки, ее скорости и силе остановки. Также, здесь мы определим закон пропорциональности между скоростью лодки и скоростью потока воды, а также предложим рекомендации для выполнения контрольных работ по математике.

Перед тем как перейти к решению задачи, обратимся к базовым понятиям. Моторная лодка движется спокойной водой скоростью, которая составляет 2,28 м/с. Вода в реке течет со скоростью 5 м/с. Для определения закона пропорциональности между скоростью лодки и скоростью течения воды, необходимо воспользоваться определением производной. В данном случае, величина производной будет равна скорости, с которой лодка движется относительно воды.

Рассмотрим движение лодки в спокойной воде подробнее. По принципу закрытого контура Бернулли, коэффициентами пропорциональности будут перемножаться скорость воды и ее плотность.

Итак, используя метод уравнений движения, можно прийти к заключению, что в данной задаче закон пропорциональности между скоростью лодки и скоростью течения воды можно определить как произведение этих двух скоростей с коэффициентами пропорциональности. Таким образом, уравнение движения лодки будет иметь вид:

Скорость лодки = Коэффициент пропорциональности * Скорость течения воды.

Ответ на задание заключается в определении закона пропорциональности, вычислении значения коэффициентов пропорциональности и предложении методов решения задачи о движении моторной лодки в спокойной воде с постоянной скоростью.

Для выполнения контрольных работ по математике вам рекомендуется учиться решать задачи по осаждению нефти и ходу катера. В энциклопедии математики вы найдете много полезной информации по данной теме.

Надеемся, что наш раздел помог вам в выполнении задания по математике. Спасибо за внимание!

Большая Энциклопедия Нефти и Газа

Для решения данной задачи используем дифференциальное уравнение. Оно выглядит следующим образом:

dF = c * v^2

где dF — изменение силы, c — постоянная, v — скорость. Из данного уравнения можно заключить, что сила сопротивления пропорциональна квадрату скорости.

Перейдем к решению уравнения. Интегрируем его по обеим сторонам:

∫dF = c * ∫v^2

F = c * (v^3)/3 + C

где F — сила сопротивления, C — произвольная постоянная интегрирования.

Итак, мы получили формулу для определения силы сопротивления движению моторной лодки. Теперь можем использовать ее для нахождения ответа на задачу. Подставив значения заданных в условии задачи, получим:

F = c * (5^3)/3 + C

Здесь c и C являются постоянными, которые должны быть определены на основе данной задачи.

Таким образом, мы определили формулу для вычисления силы сопротивления движению моторной лодки на спокойной воде. Решение данной задачи поможет студентам углубить свои знания в области дифференциальных уравнений и применения их в реальной жизни.

Спокойная вода

Математика играет важную роль в определении движения моторной лодки. Дифференциальные уравнения позволяют точно определить скорость и ход движения катера. Например, для задачи определения сопротивления катера при движении по спокойной воде существует формула, согласно которой сопротивление пропорционально скорости движения лодки.

В рамках курса «Математика в морской навигации» в Беларуском Государственном Техническом Университете (БГТУ) студентам предлагается решать задачи, связанные с определением движения лодки и сопротивления воды. Одна из задач заключается в определении скорости моторной лодки при движении по спокойной воде с заданной константой расхода топлива. Студентам необходимо найти дифференциальное уравнение, описывающее движение лодки, и решить его, чтобы определить скорость.

Кроме того, в процессе выполнения задания студентам предлагается использовать математические методы, такие как производные и интегралы. Они могут использовать различные формулы из высшей математики для решения задачи, например, формулу для определения производной функции.

Рекомендации по выполнению задания включают в себя определение конкретной точки движения лодки и необходимости найти коэффициент сопротивления воды. Кроме того, студентам предлагается использовать хэшкод задачи для контроля успешности выполнения задания.

Таким образом, спокойная вода является благоприятным условием для движения моторной лодки. Для определения хода и скорости катера на спокойной воде необходимо использовать дифференциальные уравнения и математические методы. Выполнение задач по определению движения и сопротивления воды помогает студентам углубить свои знания в математике, применяемой в морской навигации.

Источник: «Великая советская энциклопедия»

Определить силу сопротивления воды движению моторной лодки

Для определения силы сопротивления воды движению моторной лодки в спокойной воде необходимо решить задачу на основе имеющихся данных. Это важное задание, которое часто встречается при выполнении контрольных работ в высшей математике или в курсе дифференциальных уравнений.

Формула для определения силы сопротивления воды движению цилиндрического судна может быть выведена на основе закона сохранения энергии. Величина силы сопротивления пропорциональна квадрату скорости судна и площади сечения поперек течения воды.

Методика выполнения этой задачи может быть разной, в зависимости от поставленных условий задачи и требуемого результата. Например, можно использовать дифференциальное уравнение, чтобы найти ускорение лодки.

Для выполнения задачи по определению силы сопротивления воды движению моторной лодки можно использовать такие данные, как скорость моторной лодки и ее коэффициент осаждения. Зная эти значения, можно использовать формулу для определения силы сопротивления и решить уравнение для нахождения ускорения.

Примеры таких задач можно найти в учебных пособиях, в энциклопедиях или на страницах университетов и академических колледжей. В некоторых задачах будет дано судно определенной формы, например, катер, и нужно будет найти его силу сопротивления воде при движении вдоль потока.

Решения таких задач могут быть полезными при выполнении контрольных работ в высшей математике или на курсе дифференциальных уравнений. В них будет необходимо определить силу сопротивления воды движению моторной лодки и найти ее значение для заданной скорости.

Таким образом, определение силы сопротивления воды движению моторной лодки является важной задачей, и ее решение может быть полезным для практического применения при работе с моторными лодками или другими судами в воде.

Видео:

Теплоход, скорость которого в неподвижной воде равна 16 км/ч, проходит по течению реки и после

Теплоход, скорость которого в неподвижной воде равна 16 км/ч, проходит по течению реки и после by Пятью Пять 1,254 views 1 year ago 2 minutes, 46 seconds