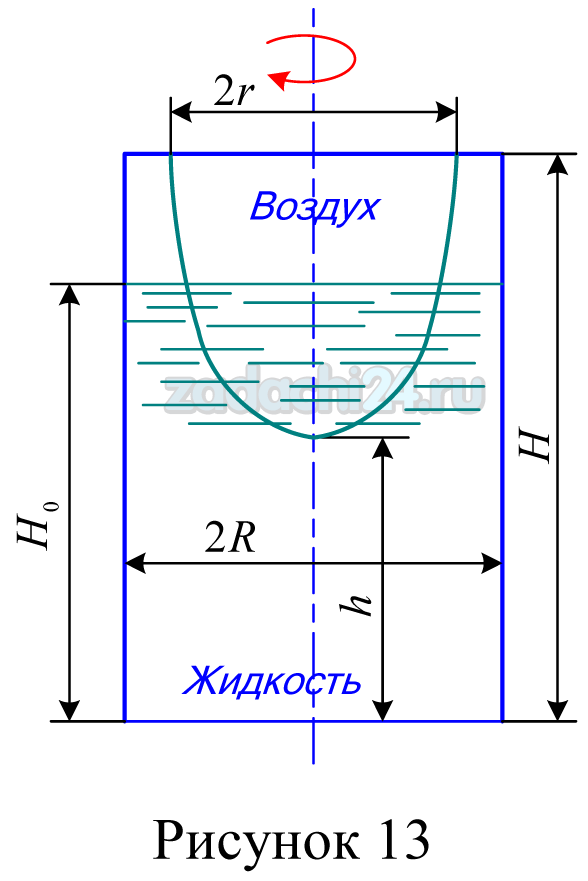
Вода в цилиндрическом сосуде начинает вращаться

Допустим, цилиндрический сосуд с водой вращается с постоянной частотой вокруг своей оси. В этом случае, высота столба воды в сосуде определяется радиусом сосуда и равномерной частотой вращения. Если взять точку на свободной поверхности воды и определить ее высоту, то можно установить зависимость между высотой и радиусом сосуда.

Запишем уравнения вращения для каждой точки жидкости с учетом силы тяжести, которой она подвержена. Получим выражение для высоты столба воды в зависимости от радиуса цилиндрического сосуда и частоты вращения. Также, если угловой наклон сосуда будет меняться постепенно, то будут меняться и высоты столба воды в разных частях цилиндрического сосуда.

Цилиндрический сосуд с водой вращается

Рассмотрим цилиндрический сосуд с водой, который вращается вокруг вертикальной оси. В данном сосуде сосредоточена жидкость. Изначально, сосуд заполнен водой до определенной высоты.

Для описания поведения жидкости внутри сосуда, запишем уравнение движения жидкости в цилиндрических координатах. Предположим, что уровень жидкости в сосуде является неподвижной точкой отсчета, и что жидкость движется вдоль радиального направления. Тогда распределение давления в сосуде определяется выражением.

Точки в системе отсчета, заданном сосудом, вращается вместе с жидкостью	Точки, где жидкость находится в состоянии покоя
Таким образом, сила, действующая на единицу столба жидкости, определяется выражением.	Если цилиндрический сосуд с водой вращается с постоянной угловой скоростью, то для точек, которые вращаются с телом, у нас есть следующие уравнения:

Для определения распределения давления в жидкости в случае вращения сосуда, запишем уравнение поверхности. Получим:

Также найдем уравнение для определения высоты столба жидкости, если вращение происходит с постоянной угловой частотой ω.

Таким образом, распределение давления в жидкости и профиль высоты столба жидкости в цилиндрическом сосуде, вращающемся вокруг вертикальной оси, будут влиять на возникающие силы и обмин внутри жидкости.

Равновесие жидкости в движущихся сосудах вращение

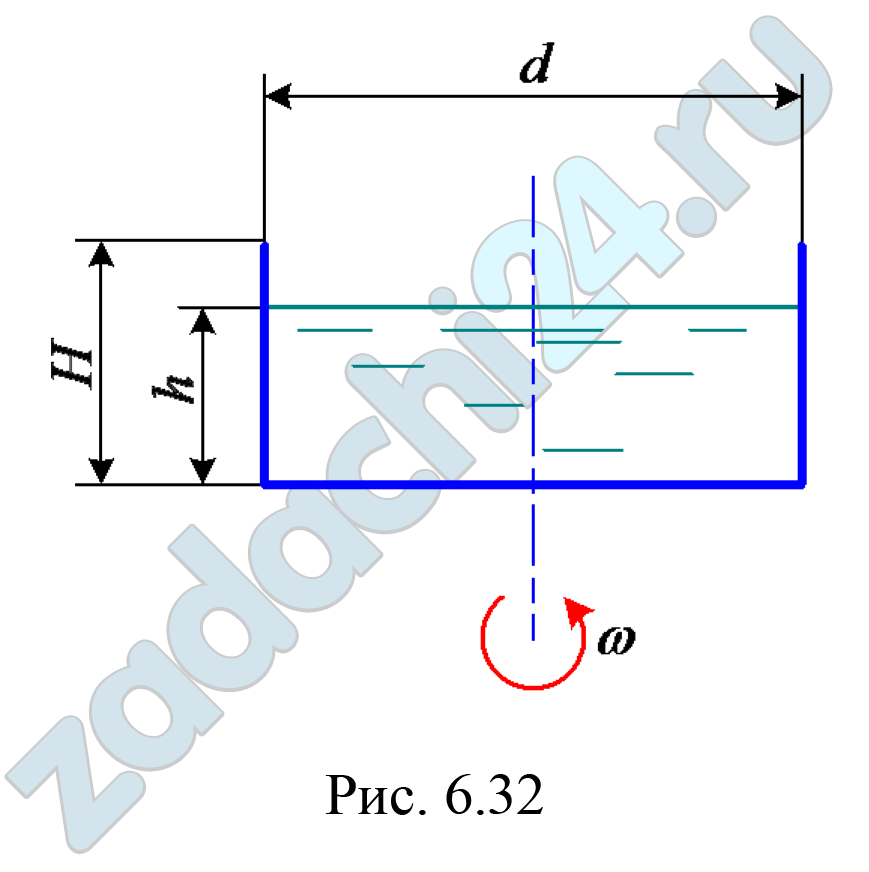
Рассмотрим цилиндрический сосуд, в котором находится вода. После того, как сосуд закрывается крышкой и начинает вращаться с заданной частотой, вода также начнет вращаться вместе с сосудом.

В данной системе силы, действующие на любую точку жидкости, можно разделить на две части: силу давления и силу центробежной силы.

Закон равномерного распределения давления в жидкости

При равномерном вращении сосуда вокруг своей оси, давление в жидкости принимает одинаковые значения на любой высоте сосуда. Это связано с тем, что сила давления в жидкости распределяется равномерно по всему объему.

Равномерное распределение давления в жидкости в движущихся сосудах вращению можно представить с помощью уравнения, которое можно получить, рассмотрев столб воды, находящийся между двумя точками на разной высоте. Давление воды в данном случае определяется как сумма двух сил: силы тяжести и центробежной силы.

Давление воды в цилиндрическом сосуде определяется выражением:

где P — давление жидкости, h — высота столба жидкости, g — ускорение свободного падения, ρ — плотность жидкости, ω — угловая скорость вращения сосуда.

Закон равномерного распределения скорости жидкости

Скорость жидкости в движущихся сосудах вращении также распределяется равномерно по сечению сосуда. Это связано с тем, что каждая точка жидкости вращается с одинаковой скоростью.

Равномерное распределение скорости жидкости в движущихся сосудах вращении можно представить с помощью уравнения:

где v — скорость движения жидкости, R — радиус сосуда, ω — угловая скорость вращения сосуда.

Таким образом, равновесие жидкости в движущихся сосудах вращение представляет собой баланс сил давления и центробежной силы, который обеспечивает равномерное распределение давления и скорости внутри сосуда.

Равномерное вращение сосуда с жидкостью

Равномерность вращения сосуда с жидкостью определяется законом сохранения момента импульса. После установления равновесия сила тяжести и сила трения, действующие на точки жидкости в различных частях сосуда, ровны между собой.

Распределение массы вращающейся жидкости в сосуде представляет собой цилиндрический столб, точки которого находятся на различных расстояниях от оси вращения. Чтобы обеспечить равное распределение массы, диаметр сосуда должен быть максимальным в его нижней части и убывать по мере подъема к верху.

Скорость вращения вокруг своей оси заданном вращающейся сосудом с жидкостью является постоянной для каждой точки жидкости. Данная скорость определяется равновесием сил тяжести и центробежной силы вращения.

Следовательно, равномерное вращение сосуда с жидкостью вокруг своей оси может быть представлено следующим образом:

Обнин характеристик жидкости в сосудах при вращении

• Высота жидкости в столбе сосуда увеличивается при увеличении радиуса
• На поверхности жидкости образуется выпуклость вверх
• Сила давления на дно сосуда увеличивается с увеличением радиуса
• Распределение давления воздуха в сосудах определяется скоростью вращения жидкости и наклону сосуда
• Частота оборотов сосуда определяется скоростью вращения жидкости и радиусом сосуда

Уравнение, описывающее равномерное вращение сосуда с жидкостью, можно запишем следующим образом:

2πRН / T = ωR

где RН — высота столба жидкости в сосудах, T — период обращения, ω — угловая скорость вращения жидкости.

В данном случае равномерное вращение сосуда с жидкостью означает, что угловая скорость вращения жидкости в сосудах является постоянной и не зависит от радиуса или высоты столба.

Равновесие жидкости в движущихся сосудах

Центробежная сила и равномерное вращение

Это явление можно объяснить с помощью таких понятий, как центробежная сила и равномерное вращение. Центробежная сила — это сила, которая действует на тело в направлении от центра вращения к его основаниям. Равномерное вращение — это такое вращение, при котором угловая скорость остается постоянной. В данном случае, вода получает такую скорость, что она остается в контакте со стенками сосуда.

Сила тяжести и сила трения, в свою очередь, пытаются оттянуть воду от стенок. Однако, эти силы компенсируются центробежной силой, которая действует на воду из-за вращающегося сосуда. После достижения равновесия, сумма всех сил, действующих на воду, становится равной нулю, что позволяет воде оставаться в состоянии покоя относительно сосуда.

Уравнение равновесия жидкости

Можно запишем уравнение равновесия для фрагмента воды в сосуде:

ΣFr = Fn + Ft + Fc = 0

где ΣFr — сумма всех сил, действующих на фрагмент воды, Fn — сила нормального давления, Ft — сила трения между водой и стенками, Fc — центробежная сила.

Используя выражение для центробежной силы Fc = mv²/r, где m — масса фрагмента воды, v — скорость вращения, r — радиус сосуда, можно провести ряд преобразований для уравнения равновесия и найти зависимость между радиусом и скоростью вращения сосуда.

Также, часто в этом случае используют понятие частоты вращения s. Частота связана со скоростью вращения следующим выражением: s = v/r.

Окончательно, после всех преобразований, уравнение равновесия можно записать в следующей форме:

m(g — s²r) = 0

где g — ускорение свободного падения.

Из этого уравнения можно заметить, что масса фрагмента воды не играет роли в равновесии, что говорит о том, что равновесие жидкости в движущихся сосудах зависит только от ускорения свободного падения, радиуса сосуда и частоты вращения.

Таким образом, равновесие жидкости в движущихся сосудах — это интересное явление, которое проявляется при вращении сосуда вокруг своей оси. Это равновесие возникает из-за компенсации центробежной силой сил тяжести и трения, и может быть описано уравнением равновесия, зависящим от ускорения свободного падения, радиуса сосуда и частоты вращения.

Видео:

ЕГЭ по математике. Базовый уровень. Задание 13. Объем цилиндра.

ЕГЭ по математике. Базовый уровень. Задание 13. Объем цилиндра. by Vyacheslav N 11,049 views 7 years ago 6 minutes, 8 seconds