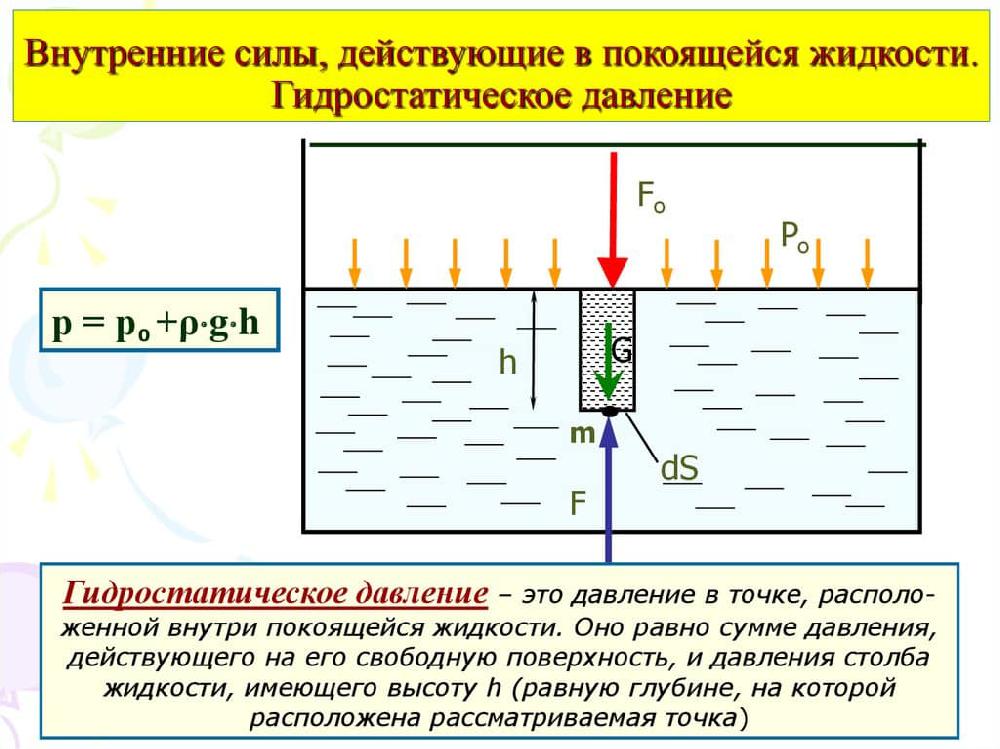
Зависимость между высотой столба и давлением воды

Одно из интереснейших и обсуждаемых вопросов в науке – зависимость высоты столба от величины водного давления. Мы все знаем, что вода проходит через трубы с большой скоростью, однако она способна удерживаться в высоких сосудах. Этот парадокс можно объяснить с помощью гидростатического давления.

Гидростатическое давление – это давление, которое оказывается на поверхность жидкости или газа под воздействием силы тяжести. Используя формулу давления, можно определить высоту столба жидкости:

P = ρgh

Где P – гидростатическое давление, ρ – плотность жидкости, g – ускорение свободного падения, h – высота столба.

С помощью этой формулы можно решить множество задач. Например, определить, насколько увеличится давление под дноем пластмассового стакана, если налить в него воду. Ведь высота столба в данном случае является важной характеристикой воды, оказывающую давление на дно стакана. Такие законы подтверждает наша жизнь, когда мы ставим предметы на стол и они оказываются на ровной почве, однаково весом и давлением.

Статика Давление покоящейся жидкости на дно и стенки сосуда гидростатическое давление

Давление покоящейся жидкости на дно и стенки сосуда называется гидростатическим давлением. Это давление обусловлено столбом жидкости, который оказывает силу на конструкцию сосуда равномерно во всех направлениях.

Гидростатическое давление возникает тогда, когда жидкость находится в покое. Закон гидростатического давления устанавливает, что давление внутри жидкости в любой точке зависит только от глубины этой точки и плотности жидкости.

Для расчета гидростатического давления можно использовать формулу Паскаля: давление равно плотности жидкости, ускорению свободного падения и глубине, на которой находится точка внутри жидкости.

Давление покоящейся жидкости оказывает силу на дно сосуда, которая равна весу столба жидкости, стоящего на площади дна. Если сосуд имеет закрытую конструкцию, то давление на дно также оказывает силу на стенки сосуда.

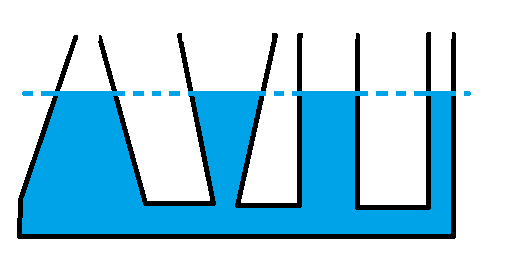
Парадокс гидростатического давления заключается в том, что давление жидкости на дно и стенки сосуда не зависит от формы и объема сосуда, а зависит только от глубины точки внутри жидкости.

Для решения парадокса можно провести эксперимент с двумя сосудами, наполненными водой, при одинаковой глубине. Расчеты покажут, что давление на дно и стенки сосудов будет одинаковым, несмотря на то, что форма и объем сосудов различны.

Для демонстрации гидростатического давления можно использовать также пробирку с песком. При наличии столба песка в пробирке можно увидеть, как давление жидкости оказывает силу на песок и его уровень в пробирке.

Гидростатическое давление на дно и стенки сосуда может быть больше или меньше, в зависимости от глубины точки внутри жидкости. Чем глубже точка, тем больше будет давление. Это объясняется формулой Паскаля, которая устанавливает, что давление жидкости на дно и стенки сосуда пропорционально глубине точки.

Таким образом, зависимость давления покоящейся жидкости на дно и стенки сосуда от глубины точки внутри жидкости объясняется законом гидростатического давления и используется для расчета давления в различных применениях, включая гидравлические системы, гидростатические испытания конструкций и другие области науки и техники.

Гидростатический парадокс

Представьте себе, что у нас есть два сосуда, соединенные трубкой. Один сосуд находится выше другого и содержит воду. Если мы создадим поперечное сечение на самом нижнем уровне воды, то давление в этом сечении будет одинаково во всех направлениях, как будто вода находится в покое.

Но если мы проделаем то же самое сечение на воде в сосуде выше, то давление будет такое же, как и в нижнем сосуде. Это может показаться странным, потому что столб воды выше и там практически нет вода. Но гидростатический парадокс гласит, что давление в жидкости зависит только от глубины и плотности жидкости, а не от объема или формы сосуда.

Этот парадокс легко объяснить с помощью закона Паскаля — давление, которое оказывает столб воды на дно сосуда, равно давлению в точке сечения. Давление передается от молекулы к молекуле через жидкость также, как передается сила на лыжах, когда мы стоим на столе. Вода оказывает силу на конструкцию в направлении относительно вертикальной вниз, но сила на столбе воды выше противодействует ей. Таким образом, площадь сечения не играет роли в законе Паскаля.

Такой парадокс можно решить с помощью расчета и заданных формул. Например, если у нас есть два сосуда, с одинаковой площадью поперечного сечения, но разной глубины, то давление на дно воды в нижнем сосуде будет такое же, как и на дне верхнего сосуда.

Итак, гидростатический парадокс позволяет нам лучше понять, как давление распространяется в жидкости. Он объясняет, почему давление в жидкости не зависит от формы или объема сосуда, а зависит только от глубины и плотности жидкости. Такой парадокс может быть интересной задачкой и вызывать удивление, но имеет простое решение с помощью закона Паскаля.

Гидростатическое давление

Определение:

Гидростатическое давление — это давление, которое создается жидкостями в статическом состоянии. Оно передается во всех направлениях и равно в любой точке данной жидкости на одной глубине.

Изучая гидростатическое давление, мы можем сделать интересное наблюдение. Представьте, что на столе в разных местах находятся три одинаковые гири (A, B, C), их суммарный вес равен 30 Н. Затем на три гири сверху положили одну гирю D, вес которой также составляет 30 Н. При этом D осталась цела, но настоящая головоломка состоит не в этом.

Задачка на гидростатическое давление:

На этом же столе налита вода такой глубины, чтобы полностью погрузить все гири. В этом случае масса воды, равная массе гири D, будет создавать давление на столе, которое в точности равно весу гири D. Вопрос заключается в том, каким будет давление на столе, если положить все гири на одну? Больше, меньше или таким же, как при размещении гирь по отдельным местам?

Казалось бы, по закону Паскаля, давление должно быть одинаково во всех точках жидкости на одной глубине. Объяснение этого парадокса состоит в том, что гири в данном случае препятствуют движению воды на столе и создают дополнительное внешнее гидростатическое давление.

Если мы рассмотрим гидростатическое давление в каждом сосуде отдельно, то сумма этих давлений должна быть равна давлению, создаваемому гирей D. Поскольку площадь дна каждого сосуда одинакова, то по формуле закона Паскаля можно определить, что давление гири на дно сосуда равно:

P = F/S

где P — давление, F — вес гири, S — площадь дна сосуда.

Поэтому, если нам задают задачу на гидростатическое давление, мы всегда можем использовать формулы для расчета давления через площадь дна сосуда.

Итак, решение задачи заключается в следующем: при размещении гирь по отдельным местам давление на столе будет больше, чем при положении всех гирь на одну. Таким образом, распределение гирь по разным местам позволяет увеличить гидростатическое давление.

Закон Паскаля

Согласно закону Паскаля, давление, создаваемое жидкостью, равно весу столба жидкости, перпендикулярного к площади сечения его основания:

P = \dfrac{F}{S}

где P – давление, F – сила, вес столба жидкости, а S – площадь основания столба.

Под влиянием давления жидкости реализуется парадокс закона Паскаля. Если через столб жидкости соединить два сосуда с разной формой и высотой, то давление в них будет одинаковой. Возможность передать давление по жидкости освободила людей от напряженной работы: так, например, применение гидравлических прессов значительно упростило работу в промышленности.

Давление в жидкости передается вместе с жидкостью во всех направлениях. Согласно закону Паскаля, давление в жидкости на любой глубине не зависит от формы и объема сосуда, но зависит только от высоты столба жидкости над этой точкой.

Рассмотрим пример: если на дно сосуда, наполненного водой, поместить ботинок, то вода в верхней точке ботинка будет оказывать давление на дно сосуда, равное давлению на дно самой жидкости.

Согласно закону Паскаля, давление в жидкости можно увеличить, уменьшив площадь сечения столба жидкости или увеличив его высоту. Таким образом, можно сформулировать закон Паскаля в виде следующей формулы:

P_2 = P_1 + \dfrac{F}{S} * h

где P₂ – давление второй точки, P₁ – давление первой точки, F – сила, h – высота столба жидкости.

Согласно закону Паскаля, давление в жидкости передаётся на все точки жидкости и на стены сосуда в поперечном направлении с равной силой.

Закон Паскаля также верен для газов, так как молекулы газа также могут передавать давление друг другу.

Рассмотрим пример с весом трактора на колесо: вес трактора равен давлению, которое он оказывает на почву через колесо. Так как площадь контакта колеса с почвой меньше, чем площадь дна топливного бака, давление, которое оказывает транспортное средство на почву, значительно больше, чем давление внутри бака.

Итак, закон Паскаля позволяет определить давление в жидкости или газе в зависимости от высоты столба и площади сечения, и объясняет силу передачи давления через жидкость или газ.

Давление

Используется закон статики и гидростатическое давление для решения заданных задач. Например, если сосуды имеют одинаковую площадь входа, то давление жидкости на стенки будет одинаковым. Однако, вес жидкости и гирю, вставленные в сосуды, будут различаться в зависимости от высоты столба и плотности жидкости. Это может быть использовано, например, для решения парадокса с гирей и ботинком, когда одна гиря столь легкая, что может быть поднята ногой, но настолько тяжелая, что ее невозможно поднять рукой.

Формула для расчета гидростатического давления может быть использована для нахождения силы, с которой вода оказывает давление на дно сосуда. Эта формула связывает давление, плотность и ускорение свободного падения. Например, в цилиндрическом сосуде с песком на дне, песок оказывает давление на стенки и дно сосуда. Поэтому, если поставить гирю на верхнюю точку сосуда, давление песка на дно сосуда останется таким же, но давление песка на стенки сосуда увеличится.

Как уменьшить или увеличить давление

Для решения этой задачи можно использовать гидростатическое уравнение Паскаля. Уравнение утверждает, что давление в жидкости передается во все направления и остается одинаковым во всех точках на одной глубине.

Определите плотность вещества, которым наполнен сосуд. Вода обладает плотностью, равной 1000 кг/м³. Теперь определите площадь дна сосуда, на которую воздействует сила тяжести. Сила тяжести равна массе жидкости, умноженной на ускорение свободного падения (9,8 м/с²). Сила тяжести может быть вычислена по формуле F = m*g, где F — сила тяжести, m — масса жидкости, а g — ускорение свободного падения.

Также рассчитайте площадь стенок сосуда. Для этого измерьте диаметр сосуда и используйте формулу площади круга (S = π*r²), где S — площадь стенок сосуда, π — число Пи (приблизительно равно 3,14), а r — радиус сосуда.

Теперь сложите силы, действующие на дно и стенки сосуда. Получите сумму этих сил. Так как давление в жидкости передается во все направления, давление на дно может быть определено, используя формулу P = F/S, где P — давление, F — сумма сил, действующих на дно, и S — площадь дна сосуда.

Чтобы уменьшить давление, можно либо уменьшить высоту столба воды, либо увеличить площадь дна сосуда, на которую давление передается. Например, можно поместить под дно стола или сосуда лыжи или ботинки, чтобы увеличить площадь дна. Также можно подложить под дно слой песка или другого материала с большей площадью, чтобы давление распределилось равномерно.

Рисунок:

Изображение демонстрирует примерный расчет давления в цилиндрическом сосуде с водой. Опыт проводится на столе, и сила тяжести передается через сосуд на стол. Результатом рассчета является значение давления в паскалях.

Таким образом, путем изменения высоты столба воды или площади дна сосуда, можно увеличить или уменьшить давление в жидкости.

Закон гидростатического давления является одним из основных законов статики и объясняет множество физических явлений, связанных с давлением в жидкостях и газах.

Задачка раз

Теперь представьте, что вместо стенки сосуда у нас лежит плоский ботинок площади S, который находится на глубине h от поверхности жидкости. В этом случае на плоский ботинок также действует гидростатическое давление с силой F, которую можно рассчитать по формуле F = P × S. Таким образом, сила, с которой жидкость оказывает давление на плоский ботинок, будет равна ρghS.

Аналогичная ситуация происходит и с телом человека, находящимся под водой. Если человек находится на глубине h под водой, то на его тело также действует гидростатическое давление с силой, которая будет равна ρghS, где S — площадь проекции человека на плоскость, перпендикулярную вертикали. Именно из-за этого вода на большой глубине оказывает на тело человека большую силу, чем на малой глубине.

Также интересный факт связан с лыжами. Когда человек катается на лыжах, то при покое или малой скорости молекулы снега оказывают на лыжи небольшую силу, которая равномерно распределена по площади контакта лыж с снегом. Но если увеличить скорость движения на лыжах, сила, с которой молекулы снега оказывают давление на лыжи, увеличивается. Это происходит из-за того, что при увеличении скорости движения на лыжах площадь контакта снега со скользящими лыжами уменьшается, и соответственно, давление на единицу площади поверхности становится больше.

Таким образом, гидростатическое давление в жидкости зависит от высоты столба жидкости, плотности жидкости и ускорения свободного падения. Зависимость давления от глубины вода может быть использована в разных областях, например, для создания погружных сосудов или измерительных приборов. Также она имеет практическое применение в сельском хозяйстве, где используется для определения плотности почвы или для регулирования полива сельскохозяйственных культур.

Видео:

Изменение атмосферного давления с высотой. География в действии!

Изменение атмосферного давления с высотой. География в действии! by GeoГРАФ 2,349 views 8 months ago 9 minutes, 12 seconds